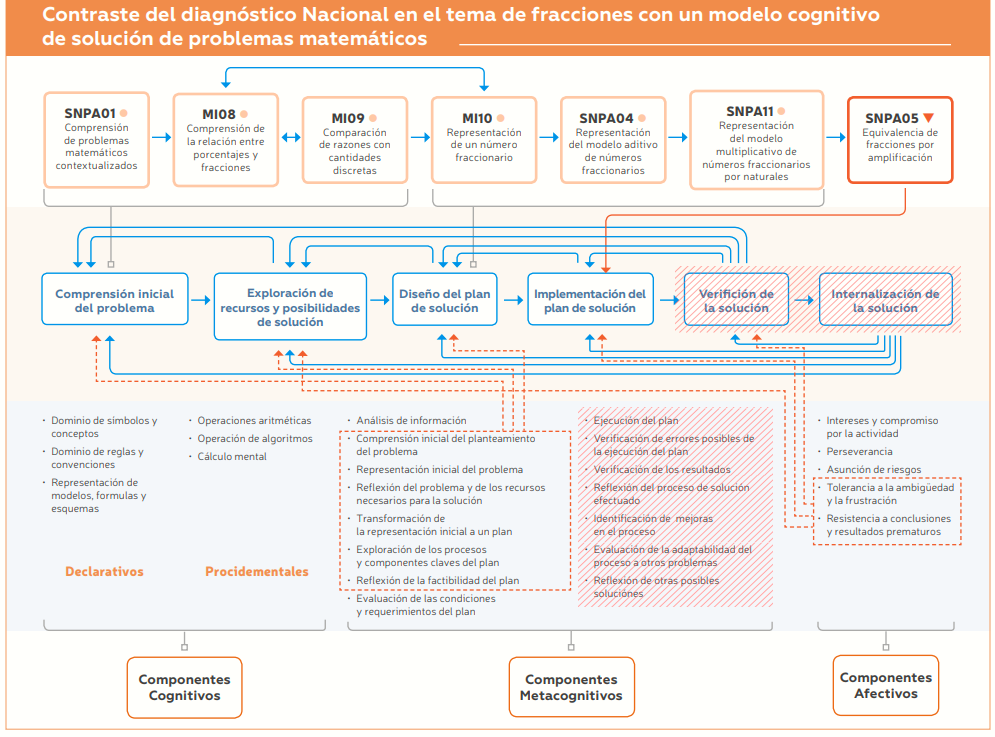
Contraste del Diagnóstico Nacional con un Modelo Cognitivo de resolución de problemas matemático

Como una primera propuesta para un reflexión a mayor profundidad con base en el contraste del diagnóstico Nacional y un modelo cognitivo, se pueden resaltar siete líneas de análisis en las habilidades básicas de Matemáticas relacionadas con:

• Conocimientos básicos de las Matemáticas (SNPA02, SNPA03, SNPA09 y SNPA10).
• Representación del conocimiento simbólico y analógico asociado a la Geometría (FEM06, FEM08 y FEM09).
• Ubicación de una coordenada en el plano cartesiano (FEM04)
• Deducción de patrones con progresiones especiales (SNPA13)
• Fracciones (SNPA01, SNPA04, SNPA05, SNPA11, MI08, MI09 y MI10)
• Medidas de tendencia central (MI03 y MI04).
• Cálculo del área de figuras geométricas (FEM11 y FEM12).

De las siete líneas de análisis mencionadas, tomando en cuenta las características estructurales e inclusoras del conocimiento y la cantidad de habilidades asociadas, se considera el tema de fracciones el más relevante para su análisis a detalle y contraste con las teorías pedagógicas, psicológicas y neurocientíficas del aprendizaje de las Matemáticas.

A continuación, se presenta un contraste del diagnóstico Nacional en el tema de fracciones con el modelo de solución de problemas matemáticos propuesto por Yimer y Ellerton (2009), así como con sus componentes cognitivos, metacognitivos y afectivos asociados. Nótese que la Equivalencia de fracciones por amplificación (SNPA05) es una habilidad básica diagnosticada con una probabilidad de dominio débil (), la cual requiere en gran medida del dominio previo de la comprensión y representación de los modelos aritméticos de las fracciones. En los reportes verbales con alumnos de Sexto de Primaria se encontró que, ante la dificultad de comprender y representar los modelos de fracciones, tendían a presentar una tolerancia baja a la ambigüedad y frustración, así como una tendencia a llegar a conclusiones y resultados prematuros. Por su parte, los alumnos con un dominio más fuerte en matemáticas presentaban una tendencia a perseverar, además de utilizar estrategias de verificación de sus soluciones y consecutivamente un ejercicio de internalización con lo que sumaban recursos que les permitía enfrentarse con más eficacia en los siguientes reactivos.